(Supporter Only) Mathematics of Recurrent Neural Networks: Backpropagation

(Supporter Only) Mathematics of Recurrent Neural Networks: Backpropagation

AI, But Simple Issue #23

This issue is a continuation of last week’s issue, where we went over the forward pass of a simple Recurrent Neural Network (RNN).

If you haven’t already, please read the last issue, as it goes over some notation, values, and understanding needed for this issue. It can be found here.

In addition to reading that issue, to get a better feeling on the process of forward propagation, backwards propagation, and neural network math, feel free to check out some of these issues listed below:

• Multi-Layer Perceptron Backwards Pass (Intermediate)

• Backpropagation, Weights, Biases (Beginner, No math)

It would also be helpful to start this issue with some knowledge of calculus and some linear algebra like matrix multiplication, but the process will still be explained to an understandable level.

Through the backpropagation process, we aim to compute the gradients of the total loss with respect to all the parameters by applying the chain rule backward through time.

• We give RNN backpropagation a special name: Backpropagation Through Time (BPTT).

As a reminder, here is the architecture of our RNN:

During the backwards pass of a neural network, the main goal is to update the weights and biases by using an optimization method such as gradient descent.

• In these optimization methods, we need to find the derivatives of the loss with respect to weights and biases, as they influence the magnitude of the weight updates.

• We need a total of 5 derivatives since there are 5 parameter matrices in total, as seen in the above neural network diagram (W_hy, W_hh, W_xh, b_y, b_h).

To find these derivatives, we need to calculate output (δy_t) and hidden errors (δh_t). Let’s get into the process.

Compute Output Errors (δy_t)

At each time step t, δy_t is calculated like so:

• p_t​: Predicted probabilities at time t.

• y_t^target : Target one-hot vector at time t.

The difference between them gives us the error at the output layer (δy_t).

Although it doesn’t matter what order you calculate the output errors, we will do so starting from the back. So working backwards, at t = 3, δy₃ is calculated as follows:

δy₃ is simply the probability distribution of the possible next words at a timestep minus the target value at the same timestep.

• As a quick reminder, the target values are taken from the original sequence “Hello World”, and the index of the target is shifted to the next word. So the y₁^target would be “Hello” and not “<START>”, and the y₂^target would be “World” and not “Hello”.

We end up with a vector of individual word errors.

We do the same thing for the next timestep, calculating the error at t = 2 (δy₂).

We repeat the same process for timestep 1 and calculate the error term δy₁:

Now that we’ve computed all the output error terms for all time steps, we can go ahead and compute gradients for the output layer parameters.

The derivative of the loss with respect to the weights of the hidden to output layer (∂L/∂W_hy) is computed as the sum of error terms multiplied by the hidden state at each time step (1, 2, and 3), transpose.

In a similar way, the derivative of the loss with respect to the output layer biases (∂L/∂b_y) is the sum of the error terms at each time step (1, 2, and 3).

As a derivation example for the derivative of the loss with respect to the weights of the hidden to output layer (∂L/∂W_hy), it takes the form shown below using the chain rule.

For cross-entropy loss using the softmax activation, the derivative of the loss with respect to the logits simplifies to:

The derivative of y_t with respect to the weights of the hidden to output layers (∂y_t/∂W_hy) simplifies to h_t.

However, since h_t doesn’t fit the size requirement for matrix multiplication, we can transpose it.

It doesn’t matter what order we compute these terms in, as long as we end up with all of them.

Now, let’s calculate the derivative of the loss with respect to weights of the hidden to output layer (∂L/∂W_hy).

Using the hidden states calculated during the forward pass (you can find the values in our previous issue), we can transpose them (for matrix multiplication purposes) and multiply them with each corresponding error term.

• As a quick reminder, in matrix multiplication, the number of columns of the first matrix must match the number of rows of the second matrix.

• In this case, the error terms will be of size 4×1, and the hidden states will be of size 2×1. In order for the matrices to be able to multiply, we can transpose the hidden state to be a size of 1×2. This way, we can multiply sizes 4×1 and 1×2 to obtain a size of 4×2.

After computing ∂L/∂W_hy, we can calculate the derivative of the loss with respect to the biases of the output layer (∂L/∂b_y).

Compute Hidden Layer Errors (δh_t)

The derivation of the hidden layer error involves recursion and other mathematical techniques, so we will skip over that for now. Simply take it at face value.

The hidden layer error at timestep t is calculated like so:

• δy_t​: Error at the output layer at time t.

• δh_t​: Error at the hidden layer at time t.

• W_hy^T​: Hidden-to-Output weights, transpose.

• W_hh^T​: Hidden-to-Hidden weights, transpose.

• tanh′: Derivative of the tanh activation function at a_t.

• ⊙: Element-wise multiplication (Hadamard product).

Where a_t is calculated like:

However, we’ve already calculated a_t for all timesteps during the forwards pass in the previous issue.

Since the hidden layer error requires h_t+1, we must work backwards starting from the last time step to calculate all the errors.

For t = 3, we have a special formula since it is the last timestep (there is no timestep 4).

So starting from the back at timestep 3, we’ll get this hidden state error (δh₃) using the special formula:

Then, we can compute δh₂ and δh₁ using the regular formula:

After computing all hidden layer error terms for all timesteps, we can now compute the derivative of the loss function with respect to the input to hidden weights (∂L/∂W_xh), hidden to hidden weights (∂L/∂W_hh), and finally the hidden layer biases (∂L/∂b_h).

As you can see from above, they are calculated using a combination of hidden state errors and other terms such as inputs and hidden states.

The derivative of loss with respect to input to hidden weights (∂L/∂W_xh) is the sum of all hidden state errors multiplied with a respective input transpose.

Similarly, the derivative of loss with respect to hidden to hidden weights (∂L/∂W_hh) is the sum of all hidden state errors at some t multiplied with a hidden state of t-1 transpose.

Finally, the derivative of loss with respect to hidden layer biases (∂L/∂b_h) is simply the sum of all hidden state errors over all timesteps.

Let’s start with computing the derivative of the loss function with respect to input to hidden weights (∂L/∂W_xh):

Then, let’s compute the derivative of loss with respect to hidden to hidden weights (∂L/∂W_hh):

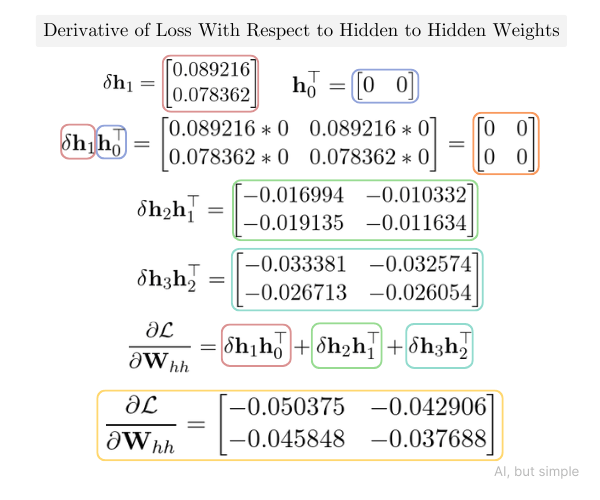
Lastly, we will compute the derivative of loss with respect to hidden layer biases (∂L/∂b_h):

At this point, we’ve finally computed all derivatives needed for parameter updates. Let’s start updating our parameters!

The new weight matrices and biases are calculated by subtracting the learning rate (η) multiplied by their respective gradients from the old weight matrices and biases.

Let’s compute the new parameters now:

Now, we’ve finally completed the backwards pass and updated all parameters. To further train the model, we can complete more forward passes and backward passes.

Here’s a special thanks to our biggest supporters:

Sushant Waidande

If you enjoy our content, consider supporting us so we can keep doing what we do. Please share this with a friend!

Feedback, inquiries, advertising? Send us an email at [email protected].

If you like, you can also donate to our team to push out better newsletters every week!

That’s it for this week’s issue of AI, but simple. See you next week!

—AI, but simple team